BARISAN dan DERET
SIMAK MATERI dibawah ini !
BARISAN
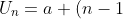b)
Keterangan:
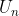 = Suku ke-n
= Suku ke-n
 = Suku pertama
= Suku pertama
 = beda (selisih suku kedua dengan suku pertama, dst)
= beda (selisih suku kedua dengan suku pertama, dst)
Contoh:
1. Perhatikan barisan berikut.
3, 7, 11, 15, ...
Tentukan: suku pertama, beda dan suku ke-15
Jawab:
a = 3,
b = U2-U1
= 7 - 3 = 4
RUMUS
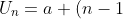b)
JAWABAN
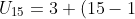4)
4=&space;3+56=59)
Barisan Geometri
2))
CONTOH SOAL dan PEMBAHASAN
1. Jumlah deret geometri tak hingga adalah 24 dan suku pertamnya adalah 16. Rasio dari deret tersebut adalah...
A.
B.
C.
D.
E.
PEMBAHASAN
Diketahui


={16})
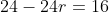
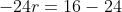
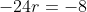


Jawaban: C

B.
C.
D.
E.
PEMBAHASAN
a = 2
b = 5-2 = 3
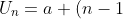b)
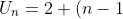3)

Jawaban: A



Jadi, n = 6 detik
Jawaban: B
4. Suku ke-5 sebuah deret aritmetika adalah 11 dan jumlah nilai suku ke-8 dengan suku ke-12 sama dengan 52. Jumlah 8 suku pertama deret tersebut adalah...
A. 72
B. 70
C. 76
D. 80
E. 86
PEMBAHASAN

+(a+11b)=52)
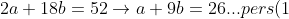)
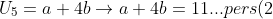)
Eliminasi variabel a dari pers (1) dan pers (2), sehingga:

Substitusi b = 3 ke pers (2), sehingga:


Jadi,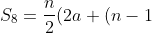b))
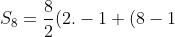3))
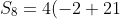)
=76)
Jawaban: C
5. Pada sebuah deret geometri diketahui bahwa suku pertamanya adalah 3 dan suku ke-9 adalah 768. Suku ke-7 deret itu adalah...
A. 36
B. 72
C. 192
D. 256
E. 64
PEMBAHASAN
a = 3
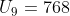

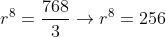
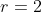
Jadi,
Jawaban: C
BARISAN
Barisan adalah daftar urutan bilangan yang mempunyai pola tertentu. Setiap bilangan dalam
barisan merupakan suku dalam barisan.
Contoh:
2,4,6,8,... dst
1,3,5,7,... dst
Ada dua jenis barisan yang akan kita bahasa satu persatu, simaklah dengan seksama.
Barisan Aritmetika
Barisan aritmetika adalah barisan dengan selisih antara dua suku yang selalu tetap. Selisih tersebut dinamakan beda dan dilambangkan dengan “b”.
Rumus Barisan Aritmatika:
Barisan Aritmetika
Barisan aritmetika adalah barisan dengan selisih antara dua suku yang selalu tetap. Selisih tersebut dinamakan beda dan dilambangkan dengan “b”.
Rumus Barisan Aritmatika:
Keterangan:
Contoh:
1. Perhatikan barisan berikut.
3, 7, 11, 15, ...
Tentukan: suku pertama, beda dan suku ke-15
Jawab:
a = 3,
b = U2-U1
= 7 - 3 = 4
RUMUS
JAWABAN
Barisan Geometri
Barisan geometri adalah barisan yang suku-sukunya diperoleh dengan
mengalikan satu bilangan tetap ke suku sebelumnya. Bilangan tetap itu
disebut pembanding atau rasio dan dilambangkan dengan r.
Barisan U1 , U2 , U3 , U4 , ….. , Un disebut barisan geometri jika memenuhi Rasio (r), dengan rasio didapat dengan: 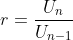
Rumus Barisan geometri:

Keterangan:
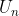 = suku ke-n
= suku ke-n
 = Suku pertama
= Suku pertama
 = rasio/pembanding
= rasio/pembanding
Contoh:
1. Tentukan suku ke tujuh dari barisan geometri 3, 6, 12, …..
Jawab:
a = 3
r = 6/3 = 2
RUMUS

JAWABAN

B. DERET
Deret adalah penjumlahan suku-suku dari suatu barisan.
Contoh:
1+2+3+4+5+...+Un
2+4+6+8+...+Un
Ada dua jenis deret yang akan kita bahasa satu persatu, simaklah dengan seksama.
Deret Aritmetika
Deret aritmetika adalah jumlah suku-suku dari suatu barisan aritmetika.
Rumus deret aritmetika:
) atau
atau 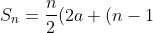b))
Keterangan:
Sn = Jumlah n suku pertama
a = suku pertama
b = beda
Contoh:
10+12=14+...+U12
Tentukan jumlah dua belas suku pertama!
Jawab:
a = 10
b = 12 - 10 = 2
RUMUS
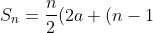b))
JAWABAN
Rumus Barisan geometri:
Keterangan:
Contoh:
1. Tentukan suku ke tujuh dari barisan geometri 3, 6, 12, …..
Jawab:
a = 3
r = 6/3 = 2
RUMUS
JAWABAN
B. DERET
Deret adalah penjumlahan suku-suku dari suatu barisan.
Contoh:
1+2+3+4+5+...+Un
2+4+6+8+...+Un
Ada dua jenis deret yang akan kita bahasa satu persatu, simaklah dengan seksama.
Deret Aritmetika
Deret aritmetika adalah jumlah suku-suku dari suatu barisan aritmetika.
Rumus deret aritmetika:
Keterangan:
Sn = Jumlah n suku pertama
a = suku pertama
b = beda
Contoh:
10+12=14+...+U12
Tentukan jumlah dua belas suku pertama!
Jawab:
a = 10
b = 12 - 10 = 2
RUMUS
JAWABAN
CONTOH SOAL dan PEMBAHASAN
1. Jumlah deret geometri tak hingga adalah 24 dan suku pertamnya adalah 16. Rasio dari deret tersebut adalah...
A.
B.
C.
D.
E.
PEMBAHASAN
Diketahui
Jawaban: C
2. Diketahui suatua barisan aritmatika :2, 5, 8, 11, 14, .........Un. Rumus suku ke-n dalam barisan aritmetika tersebut yang benar adalah...
A. B.
C.
D.
E.
PEMBAHASAN
a = 2
b = 5-2 = 3
Jawaban: A
3. Suatu jenis bakteri, setiap detik akan membelah diri menjadi dua. Jika pada saat permulaan ada 5 bakteri, waktu yang diperlukan bakteri supaya menjadi 320 adalah...
A. 5 detik
B. 6 detik
C. 7 detik
D. 16 detik
E. 20 detik
PEMBAHASAN
a = 5
r = 2
Jadi, n = 6 detik
Jawaban: B
4. Suku ke-5 sebuah deret aritmetika adalah 11 dan jumlah nilai suku ke-8 dengan suku ke-12 sama dengan 52. Jumlah 8 suku pertama deret tersebut adalah...
A. 72
B. 70
C. 76
D. 80
E. 86
PEMBAHASAN
Eliminasi variabel a dari pers (1) dan pers (2), sehingga:
Substitusi b = 3 ke pers (2), sehingga:
Jadi,
Jawaban: C
5. Pada sebuah deret geometri diketahui bahwa suku pertamanya adalah 3 dan suku ke-9 adalah 768. Suku ke-7 deret itu adalah...
A. 36
B. 72
C. 192
D. 256
E. 64
PEMBAHASAN
a = 3
Jadi,
Jawaban: C

No comments:
Post a Comment