FUNGSI KOMPOSISI

Pengertian
👉 Fungsi/Pemetaan
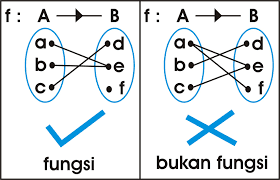
Fungsi/Pemetaan adalah relasi dua himpunan A dan B yang memasangkan setiap anggota A dengan tepat satu anggota B.

dari gambar diatas kenapa gambar yang sebelah kanan termasuk bukan fungsi ? jawabannya karena gambar seblah kanan ada anggota di himpunan A yang mempunyai 2 pasangan di himpunan B.

👀 Himpunan A disebut domain (daerah asal).

Cara penulisan domain: D = {a,b,c}

👀 Himpunan B disebut kodomain (daerah kawan).

Cara penulisan kodomain: K = {d,e,f}

👀 Himpunan anggota B yang merupakan hasil pasangan dari himpunan A disebut range (daerah hasil).

Cara penulisan range: R = {d,f}

Sifat-sifat Fungsi
1. Fungsi Injektif (satu-satu)

Dua himpunan A dan B disebut fungsi injektif apabila setiap anggota B hanya memiliki satu pasangan dengan anggota himpunan A.
🙋 Adapun contoh fungsi injektif:

👀 Gambar pertama merupakan fungsi injektif ,karena anggota himpunan B hanya memiliki satu pasangan pada himpunan A

👀 Gambar kedua merupakan fungsi injektif, karena anggota himpunan B hanya memiliki satu pasangan pada himpunan A meskipun ada satu anggota B yang tidak memiliki pasangan

👀 Gambar ketiga meupakan bukan fungsi injektif, karena ada anggota B yang memiliki dua pasangan pada himpunan A yaitu (a2, b3) dan (a3, b3)

2. Fungsi Surjektif (onto)

Dua himpunan A dan B disebut fungsi surjektif apabila setiap anggota himpunan B merupakan pasangan dari anggota himpunan A. Dengan kata lain, anggota himpunan B merupakan kodomain sekaligus range. Adapun contoh fungsi surjektif:

👀 Gambar pertama merupakan fungsi surjektif, karena semua anggota himpunan B memiliki pasangan di himpunan A

👀 Gambar kedua merupakan bukan fungsi surjektif, karena ada anggota himpunan B yang tidak memiliki pasangan di himpuanan A yaitu {s}

3. Fungsi Bijektif (korespondensi satu-satu)

Dua himpunan A dan B disebut fungsi bijektif apabila setiap anggota himpunan B mempunyai pasangan dari anggota himpunan A dan masing-masing anggotanya hanya memiliki satu pasangan. Jadi fungsi bijektif merupakan gabungan dari fungsi injektif dan surjektif.
🙋 Berikut contoh fungsi bijektif:

Gambar pertama merupakan fungsi bijektif, karena setiap anggota memiliki pasangan dan hanya memiliki satu pasangan di himpunan A
Gambar kedua merupakan bukan fungsi bijektif, karena ada anggota B yang memiliki dua pasangan di himpunan A yaitu (a,p) dan (b,p)

Jenis-jenis Fungsi
Secara garis beras fungsi fungsi terdiri dari fungsi aljabar dan fungsi transenden. Adapun yang akan kita bahas adalah jenis dari fungsi aljabar yaitu:
1. Fungsi Konstan (fungsi tetap)

Fungsi konstan adalah suatu fungsi yang memiliki nilai tetap/sama jika variabelnya disubstitusikan dengan nilai berapapun. Fungsi konstan dirumuskan f(x) = c, dengan c adalah konstanta. Grafik fungsi konstan berupa garis mendatar yang sejajar dengan sumbu x.

🙋 Contoh:
Diketahui rumus fungsi f(x) = 3 dengan daerah domain {-3,-2,-1,0,1}. Gambarkan grafiknya!

Jawab:

2. Fungsi Linear

Fungsi linear adalah suatu fungi yang memiliki grafik berupa garis lurus dengan rumus f(x) = ax + b dengan a tidak sama dengan 0.

🙋 Contoh:
DIketahui suatu fungsi f(x) = 2x + 3. Gambar grafiknya !
Jawab:

3. Fungsi Kuadrat

Fungsi kuadrat adalah suatu fungsi yang memiliki grafik berbentuk parabola, dengan rumus umum dari fungsi kuadrat $f(x)=ax^2+bx+c$ , dengan a tidak sama dengan nol.

🙋 Contoh

Fungsi f ditentukan oleh $f(x)=x^2+2x-3$ , gambar grafiknya sebagai berikut.

Fungsi Komposisi
A. Definisi
Fungsi komposisi adalah penggabungan operasi dua fungsi secara berurutan sehingga menghasilkan sebuah fungsi baru. Operasi fungsi komposisi biasanya dilambangkan dengan "o" yang dibaca komposisi/ bundaran. Bentuk umum fungsi komposisi adalah sebagai berikut.
$(fog)(x)=f(g(x))$ atau $(gof)(x)=g(f(x))$

🙋  Contoh
Diketahui dua buah fungsi yakni,
$f(x)= 3x+2$
$g(x)= 2-x$

Tentukanlah
a. $(fog)(x)$
b. $(gof)(x)$

👉 Pembahasan
$f(x)= 3x+2$
$g(x)= 2-x$

a. ( fog )( x )
( fog )(x)=f (g(x))
= 3( 2 - x ) + 2
= 6 - 3x +2
= 8 - 3x

b. ( g o f) (x)
(g o f )(x)=g ( f(x))
= 2 - ( 3x + 2 )
= 2 - 3x - 2
= - 3x

B. Nilai Fungsi Komposisi
Nilai fungsi didapat dengan mensubstitusikan nilai x pada suatu fungsi. Untuk memahami nilai fungsi komposisi, perhatian contoh berikut.

🙋  Contoh:
1. Diketahui $f(x)=5x^{2}+2$ dan $g(x)=x+1$ . Tentukan nilai $(fog)(-1)$ !

👉 Pembahasan
$(fog)(x)=f(g(x))$
$=f(x+1)$
                 $=5(x+1)^{2}+2$

$(fog)(-1)=5(-1+1)^{2}+2$

                     $=5(0)^{2}+2$

                     $=0+2=2$
🙋  Contoh:
Diketahui $f(x)=x+2$ dan $g(x)=3x$ . Tentukan nilai $(gof)(2)$ !

👉 Pembahasan
$(gof)(x)=g(f(x))$
                  $=g(x+2)$
                  $=3(x+2)$

$(gof)(2)=3(2+2)$
                 $=3(4)=12$

C. Sifat-sifat Komposisi Fungsi
1). Operasi komposisi pada fungsi-fungsi pada umumnya tidak bersifat komutatif

$(fog)(x)=\neq (gof)(x)$

2). Operasi komposisi pada fungsi-fungsi bersifat asosiatif

$(fo(goh))(x)=((fog)oh)(x)$

3). Dalam operasi komposisi pada fungsi-fungsi terdapat fungsi identitas, yaitu $f(x)=x$ sehingga berlaku

$(foI)(x)=(Iof)(x)=f(x)$

D. Menentukan Fungsi f jika fungsi g dan gof atau fog Diketahui

🙋 Contoh
1. Tentukanlah g(x) jika f(x) = 2x + 4 dan $(gof)(x)=4x^{2}+12x+6$

👉 Pembahasan
$(gof)(x)=g(f(x))=4x^{2}+12x+6$

$g(2x+4)=4x^{2}+12x+6$
Misal $y=2x+4\rightarrow x=\frac{y-4}{2}$ sehingga
$g(y)=4\left ( \frac{y-4}{2} \right )^{2}+12\left ( \frac{y-4}{2} \right )+6$

         $=4\left ( \frac{y^{2}-8y+16}{4} \right )+6(y-4)+6$

         $=y^{2}-8y+16+6y-24+6$

$g(y)=y^{2}-2y-2$
Jadi, $g(x)=x^{2}-2x-2$

🙋  Contoh
2. Diketahui $g(x)=7x-5$ dan $(gof)(x)=2x^{2}+4x-5$ . Tentukan rumus f(x) !

👉 Pembahasan
$(gof)(x)=g(f(x))=2x^{2}+4x-5$

$7(f(x))-5=2x^{2}+4x-5$

$7(f(x))=2x^{2}+4x-5+5$

Jadi, $f(x)=\frac{2x^{2}+4x}{7}$

Itulah pembahasan singkat mengenai fungsi dan fungsi komposisi, semoga postingan ini bermanfaat untuk teman-teman semua. Untuk menambah wawasan kalian, kami menyediakan beberapa tipe soal yang berkaitan dengan fungsi komposisi.

Berikut soal dan pembahasannya, yuk kita simak !

Soal dan Pembahasan
1. Diketahui $f(x)=2x+5$ dan $g(x)=x^{2}+x-4$ . Nilai dari $f(5)-2(g(-4))=$ ...

👉 Pembahasan
$f(x)=2x+5$
$f(5)=2(5)+5=10+5=15$

$g(x)=x^{2}+x-4$

$g(-4)=(-4)^{2}+(-4)-4=16-4-4=8$

$f(5)-2(g(-4))=15-2(8)=15-16=-1$

2. Jika $f(x)=3x-2$ dan $g(x)=x^{2}+1$ . Tentukan nilai $(fog)(x)+2((gof)(x))$ !

👉 Pembahasan
$(fog)(x)=f(g(x))$

                  $=3(x^{2}+1)-2$

                  $=3x^{2}+3-2=3x^{2}+1$

$(gof)(x)=g(f(x))$

                 $=(3x-2)^{2}+1$

                $=9x^2-12x+4+1$

                $=9x^2-12x+5$
Jadi, $(fog)(x)+2((gof)(x))$

          $=3x^2+1+2(9x^2-12x+5)$

     $=3x^2+1+18x^2-24x+10$

         $=21x^2-24x+11$

3. Diketahui f(x) = – 2x + 3 dan $g(x)=x^2-4x+5$ . Komposisi fungsi (gof)(x) = ...

👉 Pembahasan
$(gof)(x)=g(f(x))$
                   $=g(-2x+3)$
                   $=(-2x+3)^{2}-4(-2x+3)+5$
                  $=4x^2-12x+9+8x-12+5$
$(gof)(x)=4x^2-4x+2$

4. Jika $(fog)(x)=2x^2+4$ dan $f(x)=x-2$ maka g(x) = ...

👉 Pembahasan
$(fog)(x)=2x^2+4$
$f(g(x))=2x^2+4$
$g(x)-2=2x^2+4$
$g(x)=2x^2+4+2$
$g(x)=2x^2+6$

5. Jika $(fog)(x)=2x+4$ dan $g(x)=x+1$ maka f(x) = ...

👉 Pembahasan
$(fog)(x)=2x+4$
$f(g(x))=2x+4$

$f(x+1)=2x+4$
Misal $y=x+1\rightarrow x=y-1$ sehingga
$f(y)=2(y-1)+4$
$f(y)=2y-2+4$
Jadi,

$f(x)=2x+2$

Untuk Latihan Online Silahkan Klik di SINI

Pages

FUNGSI KOMPOSISI

No comments:

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2