TRIGONOMETRI PADA SEGITIGA

Hai Sobat, selamat datang di blog ini dan selamat belajar.

Pada kesempatan kali ini penulis akan membagikan sedikit ringkasan materi mengenai Trigonometri, oke langsung saja kita simak pemaparan materi berikut ini.

Konsep Segitiga

suatu bentuk yang dibentuk dari tiga sisi yang berupa garis lurus dan tiga sudut. Total semua sudut didalam segitiga jika ditotalkan ketiga sudutnya yaitu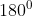 

Sejarah Singkat Trigonometri

Tahukan kalian siapa penemu rumus sinus, cosinus, tangen, secan, cosecan dan cotangen. Oke ada yang tahu siapa ?? nah ini dia penemu rumus tersebut ya dia bernama Ahmad Ibnu Abdullah Habbash Hasib Marwazi dan dikenal dengan nama Al Marwazi. Beliau lahir di Thukmenistan pada tahun 770 M dan meninggal di Samarra, Irak pada tahun 874 M.

Pengertian 

Trigonometri (dari bahasa Yunani trinom = tiga sudut dan metron = pengukuran) adalah sebuah cabang ilmu matematika yang mempelajari sudut, sisi dan perbandingan antara sudut dan sisi pada segitiga dengan menggunakan fungsi trigonometrik seperti sinus, cosinus, tangen, secan, cosecan dan cotangen.

Penerapan Trigonometri dalam Kehidupan

1. Dalam bidang kontruksi bangunan dasar dasar trigonometri sangat diperlukan seperti membuat dinding sejajar dan tegak lurus, memasang ubin keramik, kecendeerungan atap, tinggi bangunan dan masih banyak lainnya.

2. Dalam bidang arsitek juga diperlukan seperti untuk menghitung beban struktural bangunan dan sisi miring dalam sebuah bangunan, serta masih banyak lagi yang berkaitan dengan sudut sudut.

3. Dalam bidang astronomi yaitu untuk menghitung jarak ke bintang bintang terdekat bisa juga digunakan dalam sistem navigasi di laut, udara dan angkasa.

4. Dalam bidang geografi yaitu untuk menghitung antara titik tertentu dan dapat digunakan dalam sistem navigasi tertentu dalam satelit.

Perbandingan Trigonometri

Keterangan :

r : Sisi Miring

y : Sisi depan

x : Sisi Samping

 : Theta (salah satu nama sudut)

Tabel Sudut Trigonometri

Terdapat lima jenis sudut istimewa pada tabel diatas yakni 

Kuadran Trigonometri

Perhatihan 4 kuadran dibawah ini !

Kuadran I     ()

Kuadran II   ()

Kuadran III  ()

Kuadran IV  ()

Rumus Trigonometri 
Jumlah Dua Sudut dan Selisih Sudut
Sin () = sin  cos   +  cos  sin 
Sin () = sin  cos   -  cos  sin 
Cos () = cos  cos   - sin  sin 
Cos () = cos  cos   + sin  sin 

Grafik Trigonometri

• Grafik Sinus

• Grafik cosinus

• Grafik Tangen

Share this post