PELUANG - Kejadian Majemuk
Selamat datang dan Selamat belajar di KingMath, dengan belajar online semua jadi simpel. SIMAKLAH MATERI berikut ini
Terdapat 2 operasi pada kejadian majemuk, yaitu :
Macam Macam Kejadian Majemuk
Terdapat beberapa kejadian majemuk. Yuk kita pelajari lebih lanjut!
Dua Kejadian Saling Lepas adalah dua kejadian yang saling tidak mempengaruhi satu sama lain. Salah satu contoh dua kejadian saling lepas dalam kehidupan sehari seperti mandi dan tidur. Dua kejadian tersebut tidak saling mempengaruhi dan tidak dapat dilakukan dalam waktu yang bersamaan.
Keterangan:
P(A) : Peluang Kejadian A
P(B) : Peluang Kejadian B
Catatan
Peluang Kejadian A dan Peluang Kejadian B tidak ada kaitan dan hubungannya sama sekali.
RUMUS 2 KEJADIAN TIDAK SALING LEPAS
Contoh:
Dua puluh kartu diberi nomor 1 sampai dengan 20, kemudian diambil secara acak. Tentukan peluang kartu yang terambil bernomor 3 atau 5.
Jawab:
Diketahui
P(A) Peluang Kajadian A
Diketahui
P(A) Peluang Kajadian A
n( A) = kejadian terambil kartu bernomor 3 yaitu terdapat 1 buah kartu bernomor 3
n(S) = Banyaknya kartu (Banyaknya sampel) = 20 kartu
maka dengan menggunakan rumus peluang
n(S) = Banyaknya kartu (Banyaknya sampel) = 20 kartu
maka dengan menggunakan rumus peluang
dengan demikian P(A) peluang kejadian A = 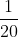
Peluang Kejadian B
n(B) = Kejadian terambil kartu bernomor 5 yaitu terdapat 1 buah kartu bernomor 5
n(S) = Banyaknya kartu (Banyaknya sampel) = 20 kartu
Peluang Kejadian B
n(B) = Kejadian terambil kartu bernomor 5 yaitu terdapat 1 buah kartu bernomor 5
n(S) = Banyaknya kartu (Banyaknya sampel) = 20 kartu
maka dengan menggunakan rumus peluang
Oleh karena A dan B adalah kejadian saling lepas maka peluang terambilnya kartu bernomor 3 atau kartu bernomor 5 adalah
2. Dua Kejadian Saling Bebas
RUMUS DUA KEJADIAN SALING LEPAS
Keterangan
P(A) : Peluang Kejadian A
P(B) : Peluang Kejadian B
Catatan Peluang Kejadian A dan Peluang Kejadian B dapat dilakukan bersamaan dalam satu waktu.
Contoh:
Terdapat 2 buah kotak, kotak A berisi 4 bola merah dan 4 bola biru. Sedangkan kotak B berisi 5 bola merah dan 2 bola biru. Jika diambil dua bola secara acak dari kejadian tersebut. Maka tentukan terambilnya 1 bola merah dari kotak A dan 2 bola biru dari kotak B !
Pembahasan
Kotak A
Mencari sampel terlebih dahulu di kotak A
4 bola merah + 3 bola biru = terdapat 7 bola di kotak A
karena yang diambilnya 1 bola merah di kotak A, maka
n(S) = 8C1=!})
= = 8
= 8
Mencari banyaknya terambilnya bola merah
n(A) = 4C1 =!})
= = 4
= 4
maka P(A) Peluang Kejadian A
Terdapat 2 buah kotak, kotak A berisi 4 bola merah dan 4 bola biru. Sedangkan kotak B berisi 5 bola merah dan 2 bola biru. Jika diambil dua bola secara acak dari kejadian tersebut. Maka tentukan terambilnya 1 bola merah dari kotak A dan 2 bola biru dari kotak B !
Pembahasan
Kotak A
Mencari sampel terlebih dahulu di kotak A
4 bola merah + 3 bola biru = terdapat 7 bola di kotak A
karena yang diambilnya 1 bola merah di kotak A, maka
n(S) = 8C1=
=
Mencari banyaknya terambilnya bola merah
n(A) = 4C1 =
=
maka P(A) Peluang Kejadian A
Kotak B
Mencari sampel terlebih dahulu di kotak B
5 bola merah + 2 bola biru = 7 bola di kotak B, maka
n(S) = 7C1 =
=
mencari banyaknya terambil bola biru
n(B) = 7C2 =
=
=
= 21
maka P(B) Peluang Kejadian B
sehingga
=

No comments:
Post a Comment